1.     Hàm Phân phối xác suất

Hàm NORMINV()

Trả về nghịch đảo của phân phối tích lũy chuẩn.

Cú pháp: = NORMINV(probability, mean, standard_dev)

probability : Xác suất ứng với phân phối chuẩn

mean : Giá trị trung bình cộng của phân phối

standard_dev : Độ lệch chuẩn của phân phối

Lưu ý:

o  Nếu có bất kỳ đối số nào không phải là số, NORMINV() sẽ báo lỗi #VALUE!

o  Nếu probability nhỏ hơn 0 hoặc lớn hơn 1, NORMINV() sẽ báo lỗi #NUM!

o  Nếu standard_dev nhỏ hơn hoặc bằng 0, NORMDINV() sẽ báo lỗi #NUM!

o  Nếu mean = 0 và standard_dev = 1, NORMINV() sẽ dùng phân bố chuẩn.

o  NORMINV() sử dụng phương pháp lặp đi lặp lại để tính hàm. Nếu NORMINV() không hội tụ sau 100 lần lặp, hàm sẽ báo lỗi #NA!

Ví dụ:

1.     Hàm Phân phối xác suất

Hàm NORMSDIST()

Trả về hàm phân phối tích lũy chuẩn tắc của phân phối chuẩn, là hàm phân phối tích lũy có giá trị trung bình cộng bằng 0 và độ lệch chuẩn là 1:

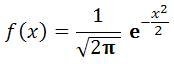
Cú pháp: = NORMSDIST(z)

z : Giá trị để tính phân phối

Lưu ý:

o    Nếu z không phải là số, NORSMDIST() sẽ báo lỗi #VALUE!

Ví dụ:

NORMSDIST(1.333333) = 0.908789 (phân phối tích lũy chuẩn tại 1.333333)

1.     Hàm Phân phối xác suất

Hàm NORMSINV()

Trả về nghịch đảo của hàm phân phối tích lũy chuẩn tắc.

Cú pháp: = NORMSINV(probability)

probability : Xác suất ứng với phân phối chuẩn tắc.

Lưu ý:

o  Nếu probability không phải là số, NORMSINV() sẽ báo lỗi #VALUE!

o  Nếu probability nhỏ hơn 0 hoặc lớn hơn 1, NORMSINV() sẽ báo lỗi #NUM!

o  NORMSINV() sử dụng phương pháp lặp đi lặp lại để tính hàm. Nếu NORMSINV() không hội tụ sau 100 lần lặp, hàm sẽ báo lỗi #NA!

Ví dụ:

NORMSINV(0.908789) = 1.3333 (nghịch đảo của phân phối tích lũy chuẩn tắc với xác suất là 0.908789)

1. Hàm AVEDEV()

Trả về sai số tuyệt đối trung bình của các điểm dữ liệu.

Để xác định được giá trị cần đo x theo một trị số trung bình, thường ta sẽ dùng một phép thử được thực hiện n lần, nhằm mục đích khắc phục những sai số ngẫu nhiên. Trong Excel, chúng ta dùng hàm AVERAGE() để tính trị số trung bình này, dựa theo công thức:

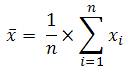
Mặc dù các sai số ngẫu nhiên của n lần thử có thể ngẫu nhiên bù trừ lẫn nhau và ta đã có được một giá trị lý tưởng x, nhưng về nguyên tắc, ta phải chấp nhận ước lượng sai số theo kiểu tối đa (sai số tuyệt đối trung bình), hay còn gọi là độ ngờ của kết quả, theo công thức:

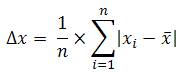
Trong Excel, chúng ta dùng hàm AVEDEV() để tính công thức này.

Cú pháp: = AVEDEV(number1, number2, ...)

number1, number2, ... : Có thể có từ 1 đến 255 đối số (con số này trong Excel 2003 trở về trước chỉ là 30). Có thể dùng mảng hoặc tham chiếu vào mảng các đối số.

Lưu ý:

o  Đối số phải là số hoặc là tên, mảng, hoặc tham chiếu có chứa số.

o  Nếu đối số là mảng hay tham chiếu mảng có chứa những giá trị text, giá trị logic, ô rỗng... thì những giá trị này sẽ được bỏ qua, tuy nhiên các ô chứa giá trị zero (0) thì vẫn được tính toán.

o  AVEDEV() luôn chịu ảnh hưởng bởi đơn vị đo lường của dữ liệu.

Ví dụ:

AVEDEV(4, 5, 6, 7, 5, 4, 3) = 1.020408 (sai số tuyệt đối trung bình của các đối số trong công thức)

1.     Hàm Thống kê

Hàm AVERAGEIF()

Trả về trung bình cộng (số học) của tất cả các ô được chọn thỏa mãn một điều kiện cho trước.

Cú pháp: = AVERAGEIF(range, criteria, average_range)

range : Là một hoặc nhiều ô cần tính trung bình, có thể bao gồm các con số, các tên vùng, các mảng hoặc các tham chiếu đến các giá trị...

criteria : Là điều kiện dưới dạng một số, một biểu thức, địa chỉ ô hoặc chuỗi, để qui định việc tính trung bình cho những ô nào...

average_range : Là tập hợp các ô thật sự được tính trung bình. Nếu bỏ trống thì Excel dùng range để tính.

Lưu ý:

o  Các ô trong range nếu có chứa những giá trị luận lý (TRUE hoặc FALSE) thì sẽ được bỏ qua.

o  Những ô rỗng trong average_range cũng sẽ được bỏ qua.

o  Nếu range rỗng hoặc có chứa dữ liệu text, AVERAGEIF sẽ báo lỗi #DIV/0!

o  Nếu có một ô nào trong criteria rỗng, AVERAGEIF sẽ xem như nó bằng 0.

o  Nếu không có ô nào trong range thỏa mãn điều kiệu của criteria, AVERAGEIF sẽ báo lỗi #DIV/0!

o  Bạn có thể các ký tự đại diện như ?, * trong criteria (dấu ? thay cho một ký tự nào đó, và dấu * thay cho một chuỗi nào đó). Khi điều kiện trong criteria là chính các dấu ? hoặc *, thì bạn gõ thêm dấu ~ trước nó.

o  average_range không nhất thiết phải có cùng kích thước với range, mà các ô thực sự được tính trung bình sẽ dùng ô trên cùng bên trái của average_range làm ô bắt đầu, và bao gồm thêm những ô tương ứng với kích thước của range. Xem ví dụ sau:

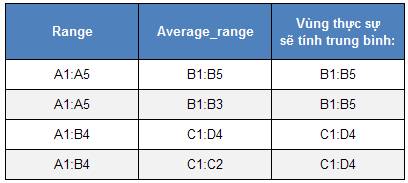
Ví dụ 1:

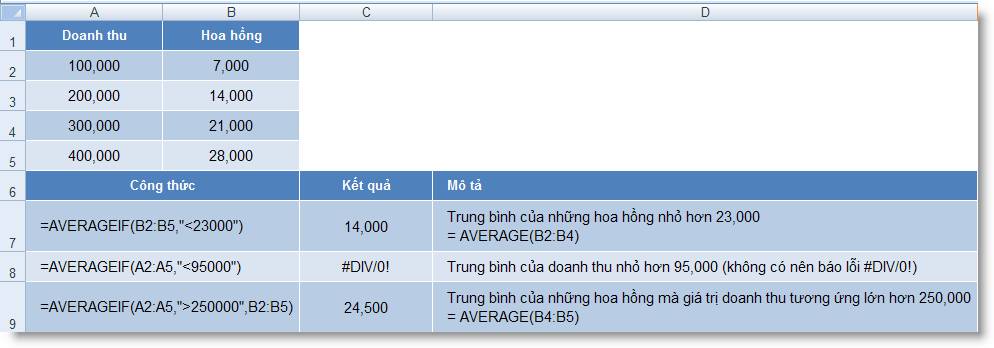
Ví dụ 2:

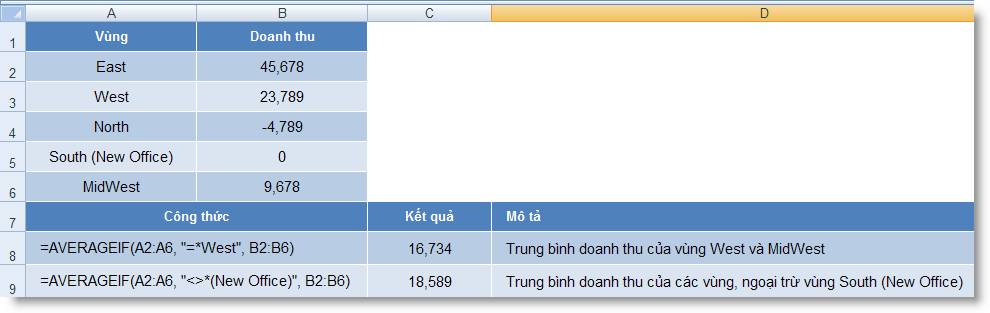
1.     Hàm Thống kê

Hàm AVERAGEIFS()

Trả về trung bình cộng (số học) của tất cả các ô được chọn thỏa mãn nhiều điều kiện cho trước.

Cú pháp: = AVERAGEIFS(average_range, criteria_range1, criteria1, criteria_range2, criteria2, ...)

average_range : Vùng cần tính trung bình, có thể bao gồm các con số, các tên vùng, các mảng hoặc các tham chiếu đến các giá trị...

criteria_range1, criteria_range2, ... : Vùng chứa những điều kiện để tính trung bình. Có thể khai báo từ 1 đến 127 vùng.

criteria1, criteria2, ... : Là các điều kiện để tính trung bình. Có thể khai báo từ 1 đến 127 điều kiện, dưới dạng số, biểu thức, tham chiếu hoặc chuỗi...

Lưu ý:

o  Nếu average_range rỗng hoặc có chứa dữ liệu text, AVERAGEIFS sẽ báo lỗi #DIV/0!

o  Nếu có một ô nào trong những vùng criteria_range rỗng, AVERAGEIFS sẽ xem như nó bằng 0.

o  Những giá trị logic: TRUE sẽ được xem là 1, và FALSE sẽ được xem là 0.

o  Mỗi ô trong average_range chỉ được tính trung bình nếu thỏa tất cả điều kiện quy định cho ô đó

o  Không giống như AVERAGEIF(), mỗi vùng criteria_range phải có cùng kích thước với average_range

o  Nếu có một ô nào trong average_range không thể chuyển đổi sang dạng số, hoặc nếu không có ô nào thỏa tất cả các điều kiện, AVERAGEIFS sẽ báo lỗi #DIV/0!

o  Có thể các ký tự đại diện như ?, * cho các điều kiện (dấu ? thay cho một ký tự nào đó, và dấu * thay cho một chuỗi nào đó). Khi điều kiện trong criteria là chính các dấu ? hoặc *, thì bạn gõ thêm dấu ~ trước nó.

Ví dụ 1:

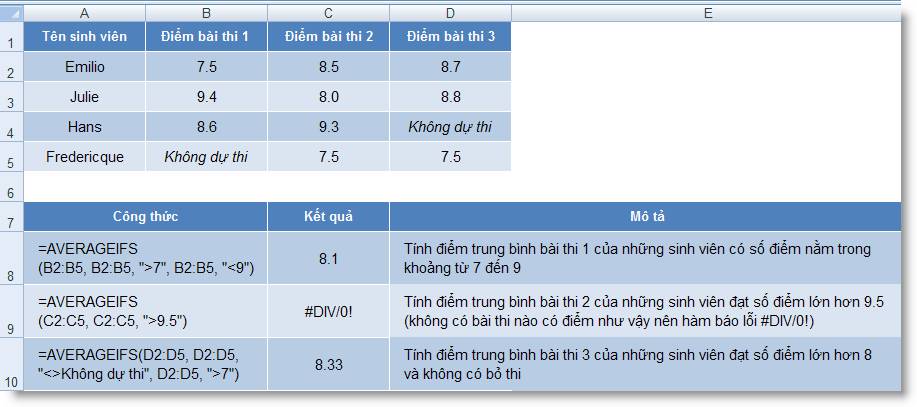
Ví dụ 2:

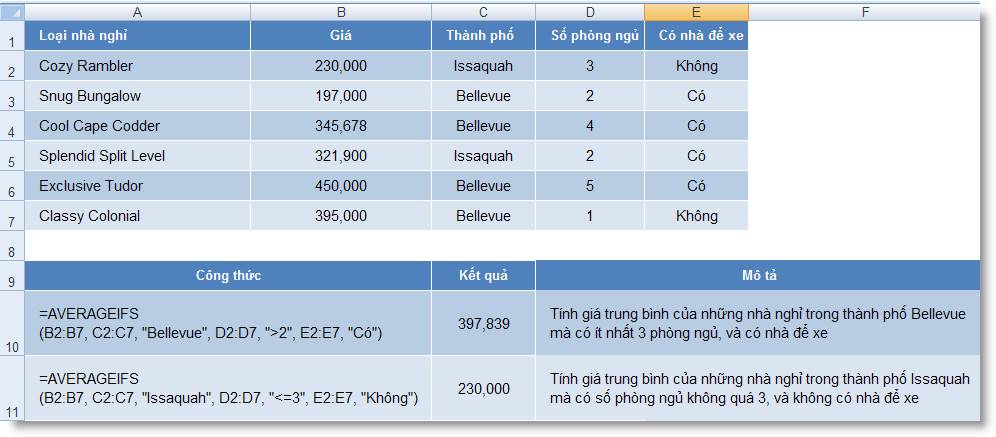
1.     Hàm Phân phối xác suất

Hàm BETADIST()

Trả về giá trị của hàm tính mật độ phân phối xác suất tích lũy beta.
Thông thường hàm này được dùng để nghiên cứu sự biến thiên về phần trăm các mẫu, ví dụ như khoảng thời gian mà người ta dùng để xem TV trong một ngày chẳng hạn.

Cú pháp: = BETADIST(x, alpha, beta, A, B)

x : Giá trị giữa A và B, dùng để tính mật độ hàm.

alpha & beta : Tham số của phân phối.

A : Cận dưới của khoảng x, mặc định là 0.

B : Cận trên của khoảng x, mặc định là 1.

Lưu ý:

o  Nếu có bất kỳ đối số nào không phải là số, BETADIST() trả về giá trị lỗi #VALUE!

o  Nếu alpha ≤ 0 hay beta ≤ 0, BETADIST() trả về giá trị lỗi #NUM!

o  Nếu x < A, x > B hay A = B, BETADIST() trả về giá trị lỗi #NUM!

o  Nếu bỏ qua A và B, nghĩa là mặc định A = 0 và B = 1, BETADIST() sẽ sử dụng phân phối tích lũy beta chuẩn hóa.

Ví dụ:

BETADIST(2, 8, 10, 1, 3) = 0.6854706

1.     Hàm Phân phối xác suất

Hàm BETAINV()

Trả về nghịch đảo của hàm tính mật độ phân phối xác suất tích lũy beta.
Nghĩa là nếu xác suất = BETADIST(x, ...) thì x = BETAINV(xác suất, ...)
Thường dùng trong việc lên kế hoạch dự án, để mô phỏng số lần mở rộng xác suất, biết trước thời gian bổ sung kỳ vọng và độ biến đổi.

Cú pháp: = BETAINV(probability, alpha, beta, A, B)

Probability : Xác suất của biến cố x trong phân phối xác suất tích lũy beta.

alpha & beta : Tham số của phân phối.

A : Cận dưới của khoảng x, mặc định là 0.

B : Cận trên của khoảng x, mặc định là 1.

Lưu ý:

o  Nếu có bất kỳ đối số nào không phải là số, BETAINV() trả về giá trị lỗi #VALUE!

o  Nếu alpha ≤ 0 hay beta ≤ 0, BETAINV() trả về giá trị lỗi #NUM!

o  Nếu probability ≤ 0 hay probability > 1, BETAINV() trả về giá trị lỗi #NUM!

o  Nếu bỏ qua A và B, nghĩa là mặc định A = 0 và B = 1, BETAINV() sẽ sử dụng phân phối tích lũy beta chuẩn hóa.

o  BETAINV() sử dụng phương pháp lặp khi tính mật độ phân phối. Với probability cho trước, BETAINV() lặp cho tới khi kết quả chính xác trong khoảng ±0.0000003. Nếu BETAINV() không hội tụ sau 100 lần lặp, nó sẽ trả về giá trị lỗi #NA!

Ví dụ:

BETAINV(0.6854706, 8, 10, 1, 3) = 2

1.     Hàm Phân phối xác suất

Hàm BINOMDIST()

Trả về xác suất của những lần thử thành công của phân phối nhị phân.
BINOMDIST() thường được dùng trong các bài toán có số lượng cố định các phép thử, khi kết quả của các phép thử chỉ là thành công hay thất bại, khi các phép thử là độc lập, và khi xác xuất thành công là không đổi qua các cuộc thử nghiệm.
Ví dụ, có thể dùng BINOMDIST() để tính xác suất khoảng hai phần ba đứa trẻ được sinh ra là bé trai.

Cú pháp: = BINOMDIST(number_s, trials, probability_s, cumulative)

Number_s : Số lần thử thành công trong các phép thử.

Trials : Số lần thử.

Probability_s : Xác suất thành công của mỗi phép thử.

Cumulative : Một giá trị logic để xác định hàm tính xác suất.

= 1 (TRUE) : BINOMDIST() trả về hàm tính xác suất tích lũy, là xác suất có số lần thành công number_s lớn nhất.
= 0 (FALSE) : BINOMDIST() trả về hàm tính xác suất điểm (hay là hàm khối lượng xác suất), là xác suất mà số lần thành công là number_s.

Lưu ý:

o  Nếu number_s và trials là số thập phân, chúng sẽ được cắt bỏ phần lẻ để trở thành số nguyên.

o  Nếu number_s, trials hay probability_s không phải là số, BINOMDIST() trả về giá trị lỗi #VALUE!

o  Nếu number_s < 0 hay number_s > trials, BINOMDIST() trả về giá trị lỗi #NUM!

o  Nếu probability_s < 0 hay probability_s > 1, BINOMDIST() trả về giá trị lỗi #NUM!

Ví dụ:

BINOMDIST(6, 10, 0.5, 0) = 0.2050781

BINOMDIST(6, 10, 0.5, 1) = 0.828125

1. Hàm CHIDIST()

Trả về xác xuất một phía của phân phối chi-squared.
Phân phối chi-squared kết hợp với phép thử chi-squared dùng để so sánh các giá trị quan sát với các giá trị kỳ vọng.
Ví dụ, một thí nghiệm về di truyền có thể giả thiết rằng thế hệ kế tiếp của các cây trồng sẽ thừa hưởng một tập hợp các màu sắc nào đó; bằng cách so sánh các giá trị quan sát được với các giá trị kỳ vọng, có thể thấy được giả thiết ban đầu là đúng hay sai.

Cú pháp: = CHIDIST(x, degrees_freedom)

x : Giá trị dùng để tính phân phối.

degrees_freedom : Số bậc tự do.

Lưu ý:

o  Nếu các đối số không phải là số, CHIDIST() trả về giá trị lỗi #VALUE!

o  Nếu x < 0, CHIDIST() trả về giá trị lỗi #NUM!

o  Nếu degrees_freedom không phải là số nguyên, phần thập phân của nó sẽ bị cắt bỏ để trở thành số nguyên.

o  Nếu degrees_freedom < 1 hay degrees_freedom > 10^10, CHIDIST() trả về giá trị lỗi #NUM!

o  CHIDIST() được tính toán theo công thức: CHIDIST = P(X > x), với X là biến ngẫu nhiên chi-squared.

Ví dụ:

CHIDIST(18.307, 10) = 0.050001