1. Hàm VAR() và VARA()

Trả về phương sai của một mẫu.

Phương sai, nói nôm na là "trung bình của bình phương khoảng cách của mỗi điểm dữ liệu tới trung bình".
Hay nói cách khác, phương sai là giá trị trung bình của bình phương độ lệch.

Hàm tính phương sai dựa theo một mẫu sẽ trả về kết quả là một con số ước lượng, được tính theo công thức:

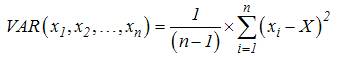
Trong đó, n là tổng số các phần tử trong mẫu và X là trung bình cộng của các phần tử trong mẫu.

Cú pháp: = VAR(number1, number2, ...)

(number1, number2, ...) : Có thể có từ 1 đến 255 đối số (con số này trong Excel 2003 trở về trước chỉ là 30)

Lưu ý:

o  VAR() giả định rằng các đối số của nó là mẫu của một tập hợp, do đó, nếu dữ liệu là toàn thể tập hợp, cần dùng hàm VARP() hoặc VARPA() để tính phương sai.

o  Trong hàm VAR(), các giá trị logic như TRUE, FALSE và các giá trị text được bỏ qua; nếu muốn tính luôn các giá trị này, bạn có thể sử dụng hàm VARA() với cú pháp tương đương.

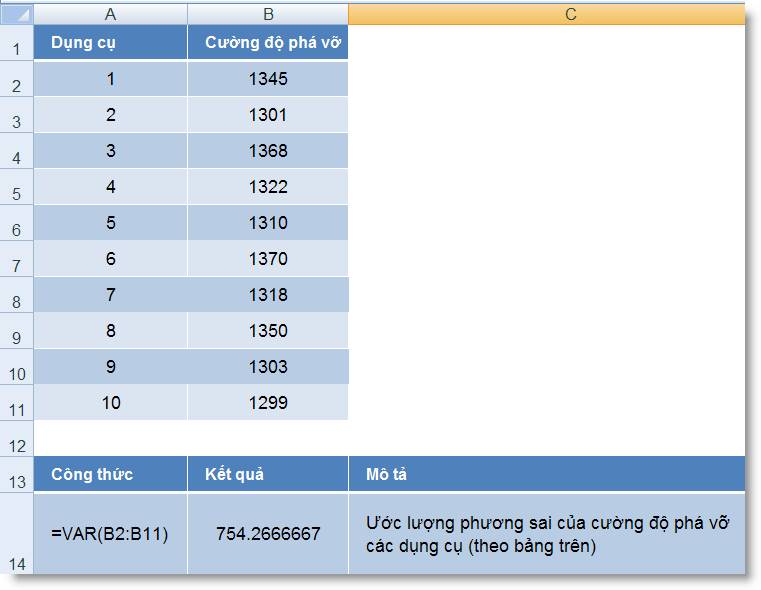
Ví dụ 1:

VAR(1, 2, 3, 4, 5) = 2.5

Thử tính lại công thức trên theo công thức:

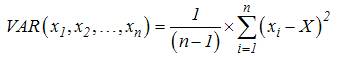
Ta có AVERAGE(1, 2, 3, 4, 5) = (1+2+3+4+5)/5 = 3

Ví dụ 2:

1. Hàm VARP() và VARPA()

Trả về phương sai dựa trên toàn thể một tập hợp.

Hàm tính phương sai dựa trên toàn thể một tập hợp sẽ trả về kết quả là một con số ước lượng, được tính theo công thức:

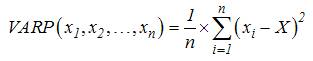
Trong đó, n là tổng số các phần tử trong tập hợp và X là trung bình cộng của các phần tử trong tập hợp. Chúng ta thấy VAR() và VARP() chỉ khác nhau ở chỗ 1/(n-1) và 1/n

Cú pháp: = VARP(number1, number2, ...)

(number1, number2, ...) : Có thể có từ 1 đến 255 đối số (con số này trong Excel 2003 trở về trước chỉ là 30)

Lưu ý:

o  VARP() giả định rằng các đối số của nó là toàn thể tập hợp, do đó, nếu dữ liệu chỉ là một số mẫu của tập hợp, ta dùng hàm VAR() hoặc VARA() để tính phương sai.

o  Trong hàm VARP(), các giá trị logic như TRUE, FALSE và các giá trị text được bỏ qua; nếu muốn tính luôn các giá trị này, bạn có thể sử dụng hàm VARPA() với cú pháp tương đương.

Ví dụ 1:

VARP(1, 2, 3, 4, 5) = 2

Thử tính lại công thức trên theo công thức:

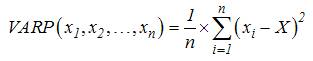
Ta có AVERAGE(1, 2, 3, 4, 5) = (1+2+3+4+5)/5 = 3

Ví dụ 2:

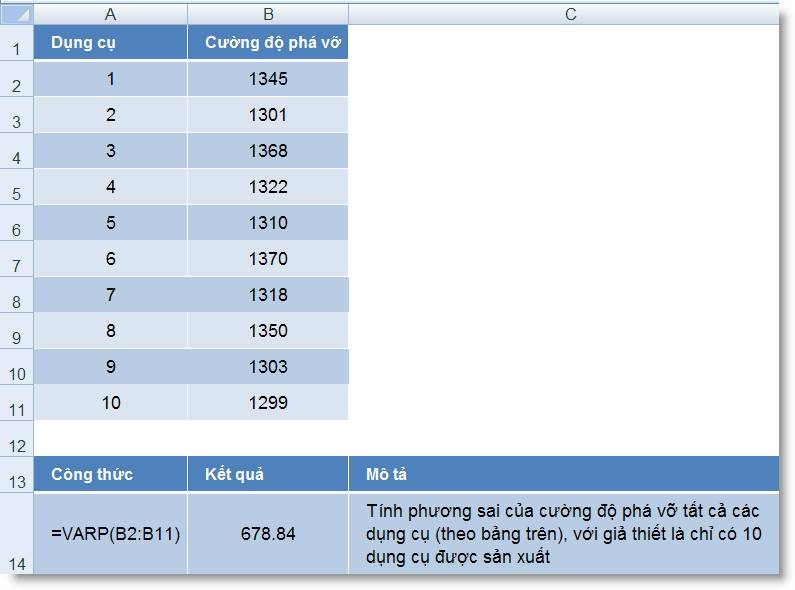
1.     Hàm Thống kê

Hàm STDEV() và STDEVA()

Ước lượng độ lệch chuẩn dựa trên cơ sở các mẫu thử của một tập hợp.

Độ lệch chuẩn, trong chứng khoán thường được dùng để đo mức độ rủi ro. Ví dụ, một cổ phiếu có tỷ suất lợi nhuận trung bình là 10%, độ lệnh chuẩn là 12%. Theo đó sẽ có 68,2% xác suất để tỷ suất lợi nhuận biến thiên trong khoảng -2% cho đến 22% và có 95,4% xác suất để tỷ suất lợi nhuận nằm trong khoảng -14% cho đến 34%. Như vậy khi độ lệch chuẩn càng cao thì khả năng "lệch" của tỷ suất lợi nhuận càng cao so với tỷ suất lợi nhuận trung bình, tức là cổ phiếu có mức độ rủi ro càng cao.[/B][/I].

Hàm tính độ lệch chuẩn dựa theo một mẫu sẽ trả về kết quả là một con số ước lượng, được tính theo công thức:

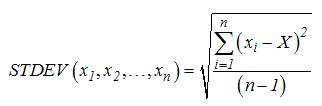
Trong đó, n là tổng số các phần tử trong mẫu và X là trung bình cộng của các phần tử trong mẫu.

Cú pháp: = STDEV(number1, number2, ...)

(number1, number2, ...) : Có thể có từ 1 đến 255 đối số (con số này trong Excel 2003 trở về trước chỉ là 30)

Lưu ý:

o  STDEV() giả định rằng các đối số của nó là mẫu của một tập hợp, do đó, nếu dữ liệu là toàn thể tập hợp, cần dùng hàm STDEVP() hoặc STDEVPA() để tính độ lệch chuẩn.

o  Trong hàm STDEV(), các giá trị logic như TRUE, FALSE và các giá trị text được bỏ qua; nếu muốn tính luôn các giá trị này, bạn có thể sử dụng hàm STDEVA() với cú pháp tương đương.

Ví dụ:

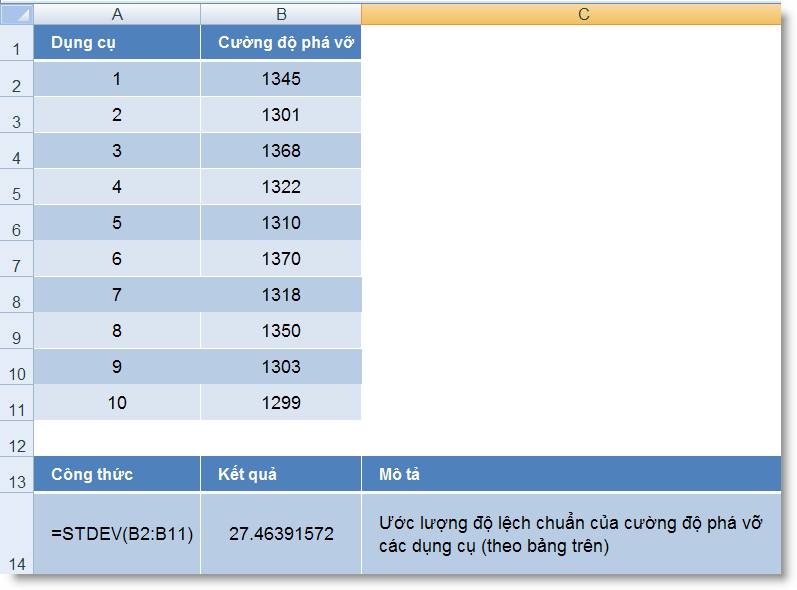
1.     Hàm Thống kê

Hàm STDEVP() và STDEVPA()

Tính độ lệch chuẩn dựa trên toàn thể một tập hợp.

Hàm tính độ lệch chuẩn dựa trên toàn thể một tập hợp được tính theo công thức:

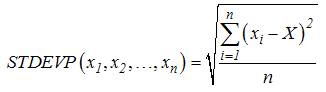
Trong đó, n là tổng số các phần tử trong tập hợp và X là trung bình cộng của các phần tử trong tập hợp.

Cú pháp: = STDEVP(number1, number2, ...)

(number1, number2, ...) : Có thể có từ 1 đến 255 đối số (con số này trong Excel 2003 trở về trước chỉ là 30)

Lưu ý:

o  STDEVP() giả định rằng các đối số của nó là toàn thể tập hợp, do đó, nếu dữ liệu chỉ là một số mẫu của tập hợp, ta dùng hàm STDEV() hoặc STDEVA() để tính độ lệch chuẩn.

o  Trong hàm STDEVP(), các giá trị logic như TRUE, FALSE và các giá trị text được bỏ qua; nếu muốn tính luôn các giá trị này, bạn có thể sử dụng hàm STDEVPA() với cú pháp tương đương.

Ví dụ:

1.     Tính toán với sự biến thiên của các giá trị

Bài viết sau đây không có tham vọng bày cho các bạn chơi chứng khoán, chỉ là để miêu tả rõ hơn về "độ lệch chuẩn" và cách sử dụng hàm STDEVP().

Cách tính giá đóng cửa điều chỉnh của các cổ phiếu (Thạc sĩ Lâm Minh Chánh)

Trong chứng khoán, giá đóng cửa điều chỉnh đóng vai trò hết sức quan trọng trong việc phân tích tỷ suất lợi nhuận của cổ phiếu. Nếu sử dụng giá đóng cửa chưa điều chỉnh, tức là giá được đăng trên bảng niêm yết giá tại sàn chứng khoán, hoặc được cung cấp bởi các công ty chứng khoán, chúng ta đã bỏ qua lợi nhuận mà nhà đầu tư thu được từ cổ tức và việc tách/thưởng cổ phiếu, vốn đóng vai trò rất quan trọng. Khi đó, việc phân tích hiệu quả đầu tư, cũng như việc so sánh giữa các cổ phiếu với nhau, việc thành lập danh mục đầu tư, hay ngay cả việc phân tích kỹ thuật, sẽ mất tính chính xác. Trong bài này, Thạc sĩ Lâm Minh Chánh sẽ trình bày tầm quan trọng và cách tính giá đóng cửa điều chỉnh của các cổ phiếu.

Cổ phiếu chúng ta lấy ra minh họa là một cổ phiếu ABC nào đó, có bảng giá đóng cửa chưa điều chỉnh trong 16 kỳ như bên dưới. Dùng 16 kỳ giá đóng cửa chưa điều chỉnh này, chúng ta tính ra kết quả tỷ suất lợi nhuận, độ lệch chuẩn của cổ phiếu như sau (xem Bảng 1):

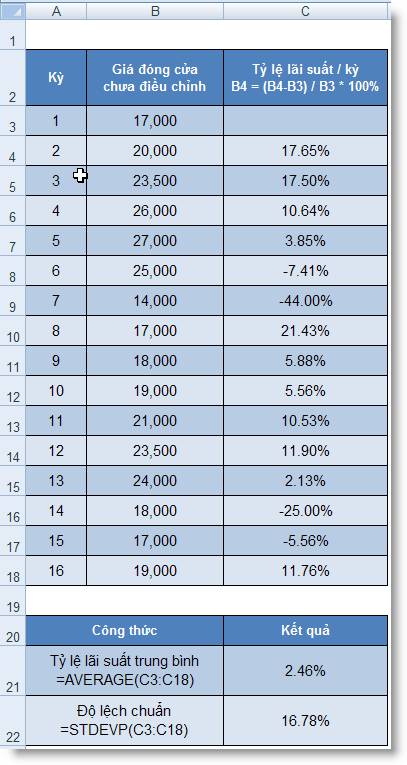
Bảng 1: Giá đóng cửa chưa điều chỉnh của cổ phiếu ABC

Việc tính toán như trên - vốn chỉ dựa vào giá đóng cửa chưa điều chỉnh - thật sự không chính xác và không thể hiện được tỷ suất lợi nhuận và độ lệch chuẩn, cũng như xu hướng giá của cổ phiếu ABC vì đã bỏ qua lợi nhuận mà nhà đầu tư nhận được việc chia cổ tức và tách thưởng cổ phiếu.

Cổ phiếu ABC có lịch chia cổ tức và cổ phiếu thưởng như sau: cuối kỳ 3, cổ tức tiền mặt 5.000; cuối đợt 7, thưởng bằng cổ phiếu: tách 1 cổ phiếu thành 2, cuối đợt 13, cổ tức tiền mặt 4.000; cuối đợt 14, thưởng bằng cổ phiếu; 2 cổ phiếu tặng 1 cổ phiếu (tức 2 thành 3).

Dựa vào những dữ liệu đó, chúng ta sẽ xác định giá đóng cửa điều chỉnh của ABC theo 2 bước như sau:

Bước 1: Tính tỷ suất lợi nhuận thật sự của cổ phiếu ABC theo từng kỳ

Thể hiện tất cả những hệ số này vào cột G (hệ số tách/thưởng cổ phiếu), cột J (cổ tức) và sử dụng những công thức thể hiện bằng chữ màu xanh trong các tiêu đề, chúng ta sẽ tìm ra được tỷ suất lợi nhuận chính xác theo từng kỳ, ở cột M. Từ đó sẽ tính được tỷ suất lợi nhuận trung bình và độ lệch chuẩn trong các ô M22 và M23 theo như bảng sau (xem bảng 2):

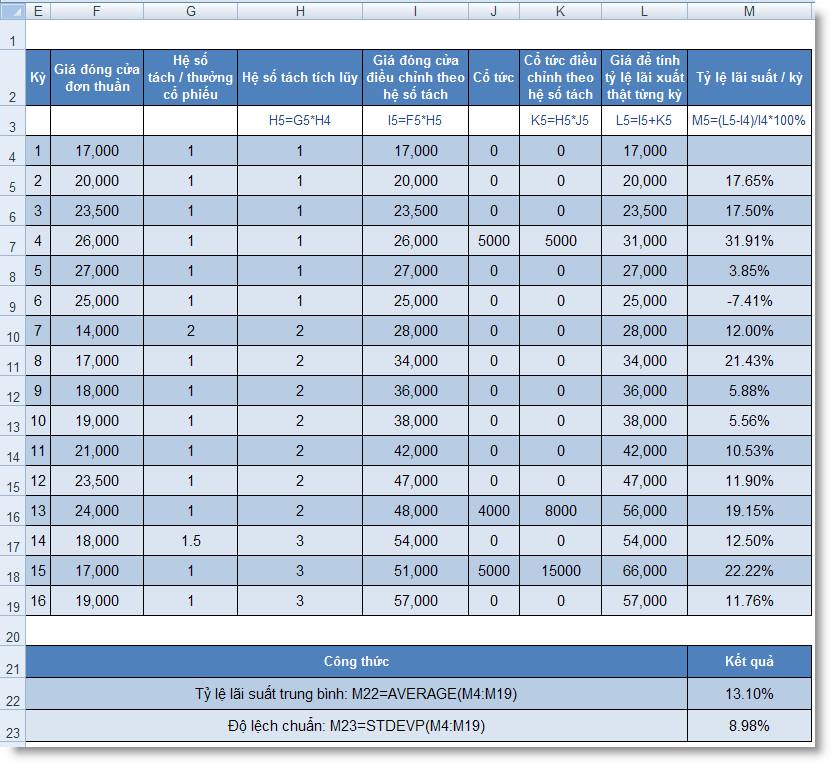
Bảng 2: Tính tỷ suất lợi nhuận thật của cổ phiếu ABC

Rõ ràng tỷ lệ lãi suất thực tính theo giá điều chỉnh đóng cửa (13,10%) cao hơn nhiều so với tỷ lệ lãi suất chỉ tính theo giá đóng cửa chưa điều chỉnh (2,46%). Độ lệch chuẩn đo mức độ rủi ro tính theo giá điều chỉnh (8,96%) cũng thấp hơn so với độ lệch chuẩn khi tính theo giá đóng cửa chưa điều chỉnh (16,78%).

Như vậy chúng ta đã tính được tỷ lệ lãi suất thật sự từng kỳ của cổ phiếu ABC. Việc còn lại là chúng ta phải thể hiện giá đóng cửa điều chỉnh như thế nào? Chúng ta không thể dùng giá tại cột L để biểu diễn giá của cổ phiếu ABC. Tại kỳ 16, giá cổ phiếu này là 19.000 chứ đâu phải 57.000.
Chúng ta sẽ tính ra giá đóng cửa điều chỉnh của cổ phiếu ABC trong vòng 16 kỳ theo cách tính ngược như sau:

Bước 2: Tính giá đóng cửa điều chỉnh của cổ phiếu ABC

Trước hết, cho giá đóng cửa điều chỉnh (ĐCĐC) cuối kỳ 16 bằng với giá đóng cửa chưa điều chỉnh cuối kỳ 16. Trên Excel, cho R18=P18. Chúng ta biết tỷ suất lợi nhuận kỳ 16 được xác định bằng công thức:

Tỷ suất lợi nhuận kỳ 16 = (Giá ĐCĐC kỳ 16 – Giá ĐCĐC kỳ 15)/Giá ĐCĐC kỳ 15*100%

Từ công thức đó ta suy ra:

Giá đóng cửa kỳ 15 = Giá ĐCĐC kỳ 16 *(1+tỷ suất lợi nhuận kỳ 16)

Áp dụng công thức này, chúng ta sẽ tính được giá đóng cửa điều chỉnh của các kỳ trước đó theo bảng sau (xem bảng 3):

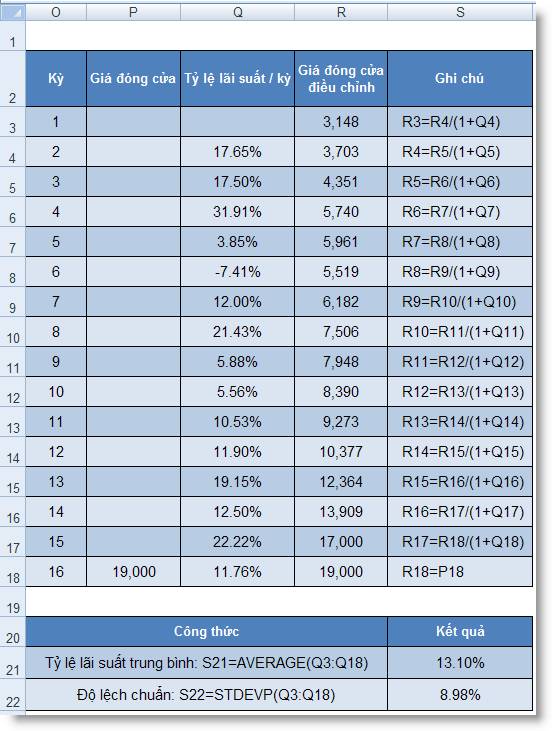
Bảng 3: Giá đóng cửa điều chỉnh của cổ phiếu ABC

Như vậy chúng ta đã có giá đóng cửa điều chỉnh trong 16 kỳ.
Minh hoạ dưới nay sẽ giúp chúng ta một lần nữa nhận rõ sự khác nhau của giá đóng cửa điều chỉnh và chưa điều chỉnh:

Giả sử chúng ta có 1.000.000 và đầu tư vào cổ phiếu ABC trong đủ 16 kỳ. Với giá đóng cửa chưa điều chỉnh, chúng ta chỉ nhận được 1.117.647 sau 16 kỳ, trong khi đó với giá đóng cửa điều chỉnh, số tiền nhận được là 6.035.800 và đây mới là con số chính xác thu được từ khoản đầu tư này (xem bảng 4).

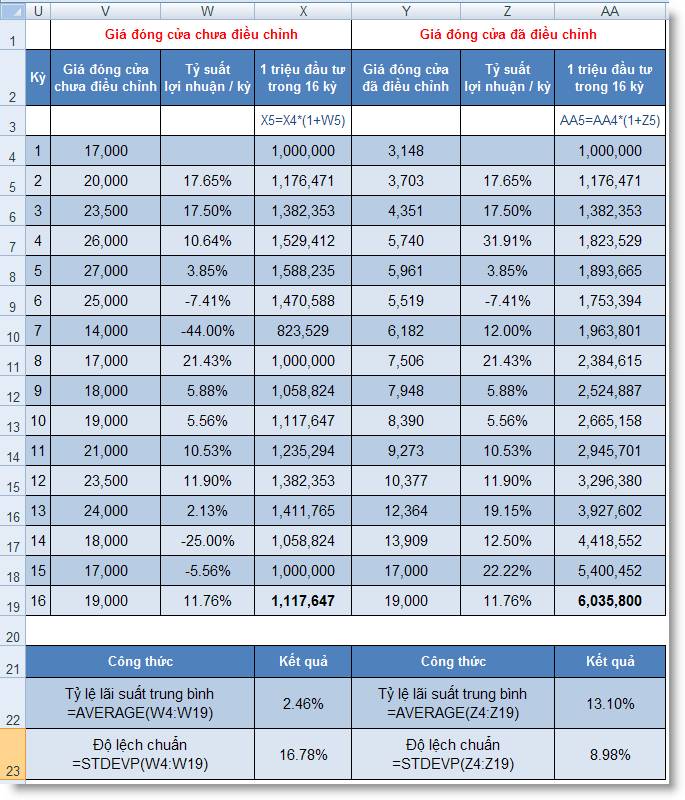
Bảng 4: Kết quả đầu tư theo 2 cách tính giá

Trước khi kết thúc, xin lưu ý các bạn ba điểm: Thứ nhất, có một vài phương cách tính giá điều chỉnh khác, tuy vậy chúng cho kết quả tương tự. Thứ hai, giá đóng cửa điều chỉnh của một cổ phiếu sẽ thay đổi khi có sự kiện chia cổ tức hay tách/thưởng cổ phiếu. Tuy vậy, tỷ suất lãi suất của từng kỳ là không thay đổi và giá điều chỉnh cuối kỳ bao giờ cũng bằng với giá đóng cửa cuối kỳ chưa điều chỉnh. Thứ ba, trong khi chờ đợi một tổ chức tại Việt Nam cung cấp giá này, từng cá nhân chúng ta có thể tính giá đóng cửa điều chỉnh để sử dụng. Điều quan trọng cần phải để ý là chúng ta phải chọn điểm xuất phát. Tốt nhất là từ ngày đầu giao dịch của cổ phiếu. Nếu không có đủ số liệu trong quá khứ, thì có thể sử dụng một ngày nào đó gần hơn, chẳng hạn 2/1/2007. Điều cần ghi nhớ là nên chọn một điểm xuất phát giống nhau cho các cổ phiếu mà chúng ta định phân tích hay thành lập danh mục đầu tư...

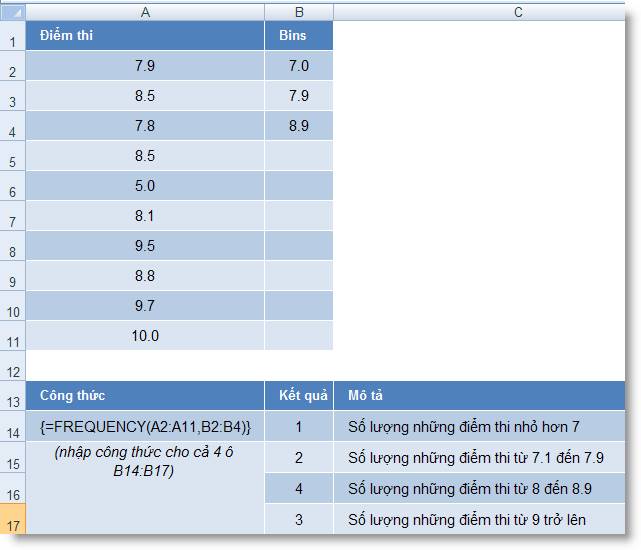
1.     Hàm Thống kê

Hàm FREQUENCY()

Dùng để tính xem có bao nhiêu giá trị thường xuyên xuất hiện bên trong một dãy giá trị, và trả về một mảng đứng các số. Trong giáo dục, FREQUENCY() thường được dùng để đếm số điểm thi nằm trong một dãy điểm nào đó, hoặc dùng để đếm (phân loại) học lực của học sinh dựa vào điểm trung bình, v.v...
FREQUENCY() là một hàm cho ra kết quả là một mảng, do đó nó phải được nhập ở dạng công thức mảng.

Cú pháp: = FREQUENCY(data_array, bins_array)

data_array : Mảng hay tham chiếu của một tập hợp các giá trị dùng để đếm số lần xuất hiện. Nếu data_array không có giá trị, FREQUENCY() trả về một mảng các trị zero (0).

bins_array : Mảng hay tham chiếu chứa các khoảng giá trị làm mẫu, và các trị trong data_array sẽ được nhóm lại theo các trị mẫu này. Nếu bins_array không có giá trị, FREQUENCY() sẽ trả về số phần tử trong data_array.

Lưu ý:

o  FREQUENCY() phải được nhập dưới dạng công thức mảng sau khi chúng ta đã chọn một dãy ô kề nhau để phân bổ sự xuất hiện của các phần tử trong mảng.

o  Số phần tử trong data_array phải nhiều hơn số phần tử trong bins_array 1 phần tử. Phần tử dôi ra này chứa số lượng các giá trị lớn hơn khoảng lớn nhất. Ví dụ, khi đếm 3 khoảng giá trị đã nhập trong 3 ô, phải chắc chắn rằng FREQUENCY() được nhập vào 4 ô; ô thứ 4 này sẽ trả về số lượng các giá trị trong data_array khi các gía trị này lớn hơn giá trị trong khoảng thứ 3. Để dễ hiểu hơn, các bạn xem ở các ví dụ sau.

o  FREQUENCY() sẽ bỏ qua các ô trống hoặc các chuỗi text.

Ví dụ:

1.     Hàm Phân phối xác suất

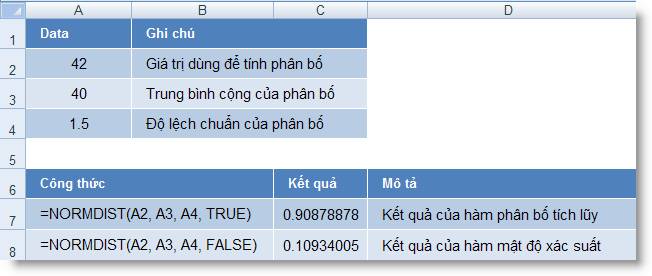
Hàm NORMDIST()

NORMDIST (= Normal Distribution) trả về phân phối chuẩn. Hàm này có ứng dụng rất rộng trong thống kê, bao gồm cả việc kiểm tra giả thuyết.

Cú pháp: = NORMDIST(x, mean, standard_dev, cumulative)

x : Giá trị để tính phân phối

mean : Giá trị trung bình cộng của phân phối

standard_dev : Độ lệch chuẩn của phân phối

cumulative : Giá trị logic xác định dạng hàm.

o    Nếu cumulative là TRUE, NORMDIST() trả về hàm tính phân phối tích lũy của phân phối chuẩn:

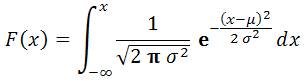
o    Nếu cumulative là FALSE, NORMDIST() trả về hàm mật độ xác suất của phân phối chuẩn:

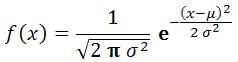
Lưu ý:

o  Nếu mean và standard_dev không phải là số, NORMDIST() sẽ báo lỗi #VALUE!

o  Nếu standard_dev nhỏ hơn hoặc bằng 0, NORMDIST() sẽ báo lỗi #NUM!

o  Nếu mean = 0 và standard_dev = 1, cumulative = TRUE, NORMDIST() sẽ trả về phân phối tích lũy chuẩn tắc (standard normal distribution) - Xem hàm NORMSDIST()

Ví dụ: