1. Tìm hiểu về vấn đề làm tròn số trong Excel

Excel có nhiều hàm dùng để làm tròn số. Mỗi hàm có một chức năng riêng.
Bài này xin nêu ra những cái khác nhau và giống nhau giữa các hàm:
ROUND(), ROUNDUP(), ROUNDDOWN(), MROUND(), CEILING(), FLOOR(), EVEN(), ODD(), INT() và TRUNC()

o  Bài tham khảo thêm: Bạn đã thử các hàm làm tròn số chưa? của chị HanDung107

Hàm ROUND()

Cú pháp: = ROUND(number, num_digits)

o  number: Con số sẽ làm tròn

o  num_digits: Là một số nguyên, chỉ cách mà bạn muốn làm tròn

num_digits > 0 : làm tròn đến số thập phân được chỉ định

num_digits = 0 : làm tròn đến số nguyên gần nhất

num_digits < 0 : làm tròn đến phần nguyên được chỉ định

Ví dụ: Với con số 1234.5678

ROUND(1234.5678, 3) = 1234.568
ROUND(1234.5678, 2) = 1234.57
ROUND(1234.5678, 1) = 1234.6
ROUND(1234.5678, 0) = 1235
ROUND(1234.5678, -1) = 1230
ROUND(1234.5678, -2) = 1200
ROUND(1234.5678, -3) = 1000

1. Hàm MROUND()

Làm tròn đến bội số của một số khác

Cú pháp: = MROUND(number, multiple)

o  number: Con số sẽ làm tròn

o  multiple: Con số mà bạn cần làm tròn number đến bội số của nó

- Nếu number và multiple khác dấu, hàm sẽ báo lỗi #NUM!
- Nếu number và multiple bằng nhau, kết quả là chính số đó
- MROUND() sẽ làm tròn lên, nếu phần chia của phép chia number cho multiple lớn hơn hoặc bằng 1/2 multiple, và làm tròn xuống nếu phần chia của phép chia number cho multiple nhỏ hơn 1/2 multiple

Ví dụ:

MROUND(5, 2) = 6 (do 5/2 > 2/2, bội số của 2 gần nhất mà lớn hơn 5 là 6)
MROUND(11, 5) = 10 (do 11/5 < 5/2, bội số của 5 gần nhất mà nhỏ hơn 11 là 10)
MROUND(13, 5) = 15 (do 13/5 > 5/2, bội số của 5 gần nhất mà lớn hơn 13 là 15)
MROUND(5, 5) = 5 (number và multiple bằng nhau)
MROUND(7.31, 0.5) = 7.5 (do 7.31/0.5 > 0.5/2, bội số của 0.5 gần nhất mà lớn hơn 7.31 là 7.5)
MROUND(-11, -5) = -10 (do -11/-5 > -5/2, bội số của -5 gần nhất mà lớn hơn -11 là -10)
MROUND(-11, 5) = #NUM! (number và multiple khác dấu)

1. Hàm ROUNDDOWN() và Hàm ROUNDUP()

Hai hàm này, về cơ bản thì giống hàm ROUND(), chỉ khác là chúng chỉ làm tròn theo một chiều: ROUNDDONW() luôn luôn làm tròn một số về số 0, còn ROUNDUP() thì luôn luôn làm tròn một số ra xa số 0.

Cú pháp:

= ROUNDDOWN(number, num_digits)
= ROUNDUP(number, num_digits)

o  number: Con số sẽ làm tròn

o  num_digits: Là một số nguyên, chỉ cách mà bạn muốn làm tròn

num_digits > 0 : làm tròn đến số thập phân được chỉ định

num_digits = 0 : làm tròn đến số nguyên gần nhất

num_digits < 0 : làm tròn đến phần nguyên được chỉ định

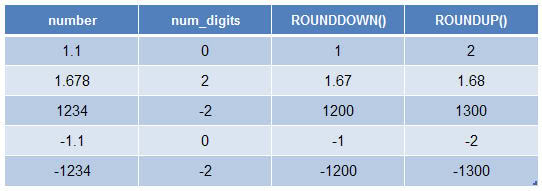
Ví dụ: So sánh giữa ROUNDDOWN() và ROUNDUP()

1. Hàm CEILING() và Hàm FLOOR()

Hai hàm này, hao hao giống hàm MROUND(), là làm tròn đến bội số gần nhất của một số được chỉ định, chỉ khác đôi chút về cách tính: CEILING() luôn luôn làm tròn một số ra xa số 0, còn FLOOR() làm tròn về số 0.

Cú pháp:

= CEILING(number, significance)
= FLOOR(number, significance)

o  number: Con số sẽ làm tròn

o  significance: Con số mà bạn cần làm tròn number đến bội số của nó

- Nếu number và significancekhác dấu, hàm sẽ báo lỗi #NUM!
- Nếu number là bội số của significance, kết quả là chính số đó

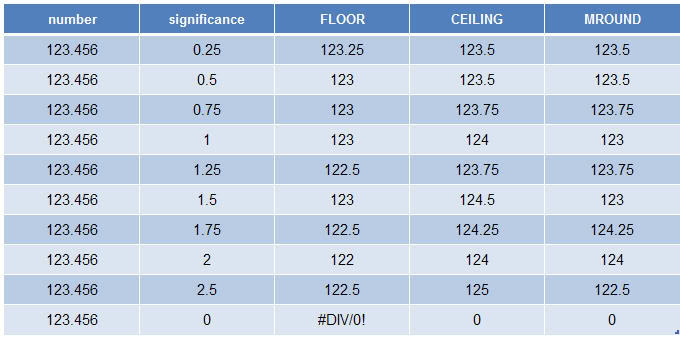
Ví dụ: So sánh giữa CEILING(), FLOOR() và MROUND() - ở ví dụ này, xem như significance là multiple của MROUND()

1. Hàm EVEN() và Hàm ODD()

Hai hàm này làm tròn rất đơn giản. EVEN() làm tròn đến số nguyên chẵn gần nhất, còn ODD() làm tròn đến số nguyên lẻ gần nhất. Cả hai đều làm tròn theo kiểu chạy xa khỏi số 0.

Cú pháp: = EVEN(number) | = ODD(number)


Ví dụ:

EVEN(14.2) = 16
EVEN(-23) = 24
ODD(58.1) = 59
ODD(-6) = -7

1. Hàm INT() và hàm TRUNC()

Hai hàm này gần như giống nhau nếu như bạn muốn làm tròn một số thành một số nguyên.

Cú pháp:

= INT(number)

= TRUNC(number [, num_digits])

o    number: Số cần làm tròn

o    num_digits: Là một số nguyên, chỉ cách mà bạn muốn cắt bớt số

num_digits > 0 : nếu number là một số thập phân, thì num_digits chỉ ra số con số thập phân mà bạn muốn giữ lại (sau dấu phẩy)

num_digits = 0 hoặc không nhập: cắt bỏ hết phần thập phân của number (nếu có)

num_digits < 0 : làm tròn number thành một số nguyên và làm tròn number sang trái thành một bội số của 10 (xem thêm ở ví dụ)

Hàm INT() làm tròn một số tới số nguyên gần nhất

Đối với số dương, hàm INT() và TRUNC() cho kết quả giống nhau (num_digits của TRUNC() = 0 hoặc không có), nhưng đối với số âm thì hai hàm này sẽ cho kết quả hoàn toàn khác nhau.

Ví dụ:

INT( 123.456) = 123 | TRUNC( 123.456) = 123

INT(-123.456) = -124 | TRUNC(-123.456) = -123

Khi num_digits khác 0, TRUNC() khác hẳn với ROUND() ở chỗ: ROUND() thì làm tròn, còn TRUNC() chỉ cắt bỏ bớt số chứ không làm tròn.

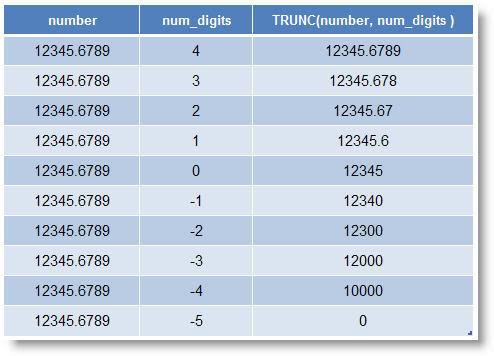
Một số ví dụ về hàm TRUNC()

1. Dùng TRUNC() để sửa lỗi Excel

Excel có một số lỗi rất vô duyên mà chắc hẳn trong chúng ta ai cũng vài lần nhức đầu với nó. Nhất là khi làm việc với số thập phân.

Tôi xin nêu một ví dụ rất nhỏ: Đố bạn 2.02 trừ 2.01 bằng bao nhiêu ? Chắc các bạn sẽ cười. Con nít cũng biết:

2.02 - 2.01 = 0.01

Nhưng Excel thì không biết ! Các bạn thử nhập phép tính 2.02 - 2.01 vào một ô nào đó, rồi cho ô này có 16 số lẻ xem, các bạn sẽ thấy Excel làm toán:

2.02 - 2.01 = 0.0100000000000002

Sao đây? Nếu các bạn dùng kết quả của 2.02-2.01 làm một tham số của VLOOKUP(), các bạn có nhận được kết quả chính xác không ?

Để chắc ăn, tôi dùng cái này:

= TRUNC(2.02 - 2.01, 2) = 0.01

Bây giờ thì định dạng ô đó có đến 100 số lẻ cũng vẫn đúng.

1. Hàm SUM()

Khi cộng các giá trị với nhau trong Excel, ta có thể dùng dấu cộng (+) hoặc dùng hàm SUM()

Cú pháp: = SUM(number1 [, number2...])

Trong Excel 2007, bạn có thể dùng SUM() để để tính tổng của 255 giá trị lại với nhau (trong những version trước, con số này chỉ là 30)

Ví dụ: = SUM(A2:A13, C2:C13, E2:E13)

1. Hàm MOD()

Dùng để lấy số dư của một phép chia

Cú pháp: = MOD(number, divisor)

number: Số bị chia
divisor: Số chia

Ví dụ: MOD(24, 10) = 4 (24 chia 10 được 2, dư 4)

1. Cộng các ô cách nhau một số hàng cố định

Có một bài toán như sau:

Trong một cột dữ liệu, người ta muốn tính tổng của cách ô cách nhau mỗi n hàng nào đó.
Ví dụ, trong dãy A1:A20, tính tổng của các ô cách nhau 5 ô, nghĩa là lấy A1 + A6 + A11 + A16

Nói tới hàng, ta nghĩ đến hàm ROW(): ROW(A1) = 1, ROW(A6) = 6, v.v...

Và ở ví dụ vừa nêu trên đây, ta để ý các con số 1, 6, 11, 16 khi đem chia cho 5 đều dư 1, vậy ta nghĩ đến hàm MOD(), lấy số thứ tự của hàng chia cho 5: MOD(ROW(A1), 5) = 1, MOD(ROW(A6), 5) = 1, v.v...

Vậy ta sẽ lập công thức cho mảng A1:A20:
Xét trong khối A1:A20, ô nào có số thứ tự của hàng chia cho 5 mà dư 1, thì lấy các ô đó cộng lại:

{= SUM(IF(MOD(ROW(A1:A20), 5) = 1, A1:A20, 0))}

Hay cụ thể hơn, gọi dãy ô để tính tổng là range, và số hàng cách nhau giữa các ô là n, ta sẽ có công thức:

{= SUM(IF(MOD(ROW(range), n) = 1, range, 0))}

Con số 1 ở đây không phải là con số cố định, mà nó là số dư của phép chia của số thứ tự cho n. Do đó, tùy vào điều kiện của bài toán mà ta thay bằng con số thích hợp.
Chẳng hạn, cũng ví dụ trên đây, như ta muốn tính tổng của các ô A2, A7, A12, A17 thì công thức sẽ là:

{= SUM(IF(MOD(ROW(A1:A20), 5) = 2, A1:A20, 0))}

(2 là số dư của 2, 7, 12, 17 cho 5)

Cộng các ô có số thứ tự hàng là chẵn, hoặc có số thứ tự hàng là lẻ

Từ bài toán trên đây, ta có công thức để cộng các ô có số thứ tự hàng làm chẵn:

{= SUM(IF(MOD(ROW(Range), 2) = 0, Range, 0))}

Và công thức để cộng các ô có số thứ tự hàng làm lẻ:

{= SUM(IF(MOD(ROW(Range), 2) = 1, Range, 0))}

1. Xem một năm có phải là năm nhuận hay không

Nếu bạn muốn có một công thức để xem thử một năm nào đó có phải là năm nhuận hay không, bạn có thể dùng hàm MOD().
Năm nhuận, là năm chia hết cho 4, hay phép dư của phép chia số năm cho 4 thì bẳng 0 ở công thức sau đây:

= MOD(year, 4)

Số năm phải là một con số có 4 chữ số.

Công thức trên chỉ đúng trong khoảng từ năm 1901 đến 2099 (có lẽ chúng ta cũng sống tối đa trong khoảng thời gian này thôi). Công thức này không đúng với năm 1900 và 2100, bởi vì điều kiện để tính năm nhuận còn có chuyện: Năm nhuận là năm chia hết cho 4, nếu năm này tận cùng bằng hai con số 0 thì nó phải chia hết cho 400 (ví dụ, năm 2000).

Vậy, để có một công thức đúng cho tất cả mọi năm, ta làm một công thức luận lý như sau:

= (MOD(year, 4) = 0) - (MOD(year, 100) = 0) + (MOD(year, 400) = 0)

Nếu công thức này cho đáp số là 1 (TRUE), thì đó là năm nhuận, còn nếu cho đáp số là 0 (FALSE), thì đó không phải là năm nhuận.

1. Ứng dụng của hàm MOD() trong định dạng bảng tính

Chắc cũng có một lúc nào đó, bạn thích định dạng cho bảng tính của mình theo kiểu Ledger Shading. Ledger Shading là kiểu định dạng các hàng có màu xen kẽ nhau (ví dụ, xanh và trắng). Loại định dạng này thích hợp cho những danh sách dài, có nhiều cột, giúp ta phân biệt được hàng này với hàng kia cách dễ dàng, ít khi bị nhìn lầm dữ liệu giữa các hàng...

Hình sau đây là một ví dụ:

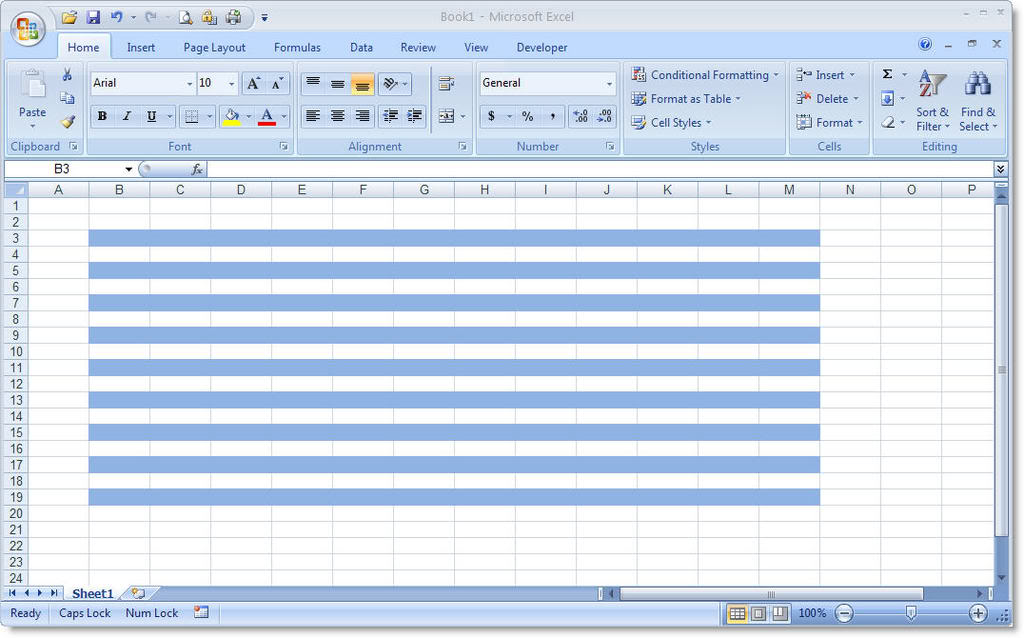
Dĩ nhiên là việc này rất dễ thực hiện, chúng ta chỉ cần chọn các hàng xen kẽ nhau và tô màu cho nó. Tuy nhiên, nếu làm thủ công bằng tay, thì sẽ có một số bất tiện sau:

- Rất lâu cho những bảng dữ liệu lớn.

- Mỗi khi chèn thêm một hàng hoặc xóa bớt một hàng, thì phải định dạng lại.

Để tránh những bất tiện đó, bạn có thể dùng một liên kết giữa hàm MOD() và chức năng Conditional Formatting (định dạng có điều kiện) của Excel.

Cách làm như sau:

1.     Chọn vùng bạn muốn định dạng

2.     Gọi hộp thoại Conditional Formatting, và chọn New Ruler để mở hộp thoại New Formatting Ruler

3.     Chọn Use a Formula to Determine Which Cells to Format

4.     Trong khung Format values where this formular is true, gõ công thức = MOD(ROW(), 2)

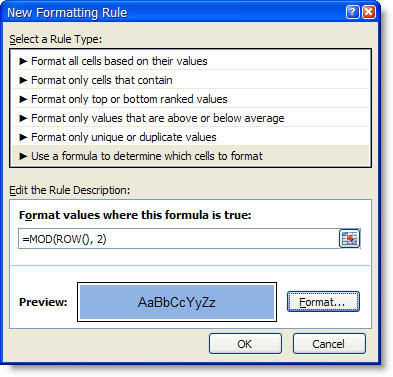
5.     Nhấn nút Format... để mở hộp thoại Format Cells

6.     Chọn tab Fills, chọn màu bạn thích tô cho các hàng xen kẽ với màu trắng, rồi nhấn OK để quay về hộp thoại New Formatting Ruler

7.     Nhấn OK

Công thức = MOD(ROW(), 2) sẽ trả về 1 cho những hàng có số thứ tự lẻ và trả về 0 cho những hàng có số thứ tự chẵn. Bởi vì 1 thì tương đương với TRUE, nên Excel sẽ áp dụng màu tô mà bạn đã chọn cho tất cả những hàng có số thứ tự lẻ trong vùng bạn muốn định dạng, và bỏ qua những hàng có số thứ tự chẵn.


Tương tự,

o    Nếu muốn định dạng các cột có màu xen kẽ, bạn chỉ cần thay công thức ở trên thành:
= MOD(COLUMN(), 2)

o    Nếu thích định dạng cho hàng có số thứ tự lẻ thì không tô màu, còn hàng có số thứ tự chẵn mới tô màu, bạn thay đổi công thức trên một tí:
= MOD(ROW() + 1, 2)

2. Hàm CHOOSE

Đây là một trong những hàm dò tìm đơn giản nhất, thường dùng để chọn một giá trị trong một danh sách.

Cú pháp: CHOOSE(index_num, value1, [value2]...)

index_num : Là vị trí của giá trị cần trả về trong danh sách. Ví dụ, index_num = 1 thì lấy giá trị value1; index_num bằng 2 thì lấy giá trị value2... Index_Num phải là một số nguyên (hoặc là một công thức là đáp số là số nguyên), và trong khoảng từ 1 đến 29

value : Danh sách các giá trị để chọn. Tối đa là 29. Những giá trị này có thể là con số, là chuỗi, là một vùng tham chiếu, là một công thức, là một hàm...

Ví dụ: Công thức = SUM(CHOOSE(a, A1:D1, A2:D2, A3:D3))
Có nghĩa là: Nếu a bằng 1, thì lấy tổng của A1:D1, nếu a bằng 2 thì lấy tổng của A2:D2, nếu a bằng 3 thì lấy tổng của A3:D3

1. Hàm RAND()

Cú pháp: = RAND()

Hàm RAND() trả về một con số ngẫu nhiên lớn hơn hoặc bằng 0 và nhỏ hơn 1. Nếu dùng hàm để lấy một giá trị thời gian, thì RAND() là hàm thích hợp nhất.

Bên cạnh đó, cũng có những cách để ép RAND() cung cấp cho chúng ta những con số ngẫu nhiên nằm giữa hai giá trị nào đó.

o  Để lấy một số ngẫu nhiên lớn hơn hoặc bằng 0 và nhỏ hơn n, ta dùng cú pháp:

RAND() * n

Ví dụ, công thức sau đây sẽ cung cấp cho chúng ta một con số ngẫu nhiên giữa 0 và 30:

= RAND() * 30

o  Trường hợp khác, mở rộng hơn, chúng ta cần có một con số ngẫu nhiên lớn hơn hoặc bằng số m nào đó, và nhỏ hơn số n nào đó, ta dùng cú pháp:

RAND() * (n - m) + m

Ví dụ, để lấy một số ngẫu nhiên lớn hơn hoặc bằng 100 và nhỏ hơn 200, ta dùng công thức:

= RAND() * (200 - 100) + 100

1.     Lấy một số ngẫu nhiên

Ở bài trên, tôi đã trình bày cách lấy một số ngẫu nhiên nằm trong một khoảng {n, m} nào đó:

= RAND() * (n - m) + m

Có một hàm nữa trong Excel có chức năng tương tự công thức trên: Hàm RANDBETWEEN().
RANDBETWEEN() chỉ khác RAND() ở chỗ: RANDBETWEEN() cho kết quả là số nguyên, còn RAND() thì cho kết quả vừa là số nguyên vừa là số thập phân.


Hàm RANDBETWEEN()

Hàm RANDBETWEEN() trả về một số nguyên ngẫu nhiên nằm trong một khoảng cho trước.

Cú pháp: = RANDBETWEEN(bottom, top)

bottom: Số nhỏ nhất trong dãy tìm số ngẫu nhiên (kết quả sẽ lớn hơn hoặc bằng số này)

top: Số lớn nhất trong dãy tìm số ngẫu nhiên (kết quả sẽ nhỏ hơn hoặc bằng số này)

Ví dụ: = RANDBETWEEN(0, 59) sẽ cho kết quả là một số nguyên nằm trong khoảng 0 tới 59.

1. Hàm ABS()

Lấy trị tuyệt đối của một số

Cú pháp: = ABS(number)

number: Số muốn tính trị tuyệt đối

Ví dụ:

ABS(2) = 2

ABS(-5) = 5

ABS(A2) = 7 (A2 đang chứa công thức = 3.5 x -2)

1. Hàm COMBIN()

Trả về số tổ hợp của một số phần tử cho trước

Cú pháp: = COMBIN(number, number_chosen)

number: Tổng số phần tử

number_chosen: Số phần tử trong mỗi tổ hợp

Chú ý:

o  Nếu các đối số là số thập phân, hàm chỉ lấy phần nguyên

o  Nếu các đối số không phải là số, COMBIN sẽ báo lỗi #VALUE!

o  Nếu number < 0, number_chosen < 0, hoặc number < number_chosen, COMBIN sẽ báo lỗi #NUM!

o  Tổ hợp khác với hoán vị: Tổ hợp không quan tâm đến thứ tự của các phần tử trong mỗi tổ hợp; còn hoán vị thì thứ tự của mỗi phần tử đều có ý nghĩa.

o  COMBIN được tính như công thức sau đây (với n = number, k = number_chosen)

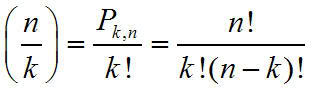
Trong đó:

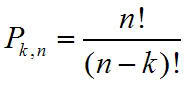
Ví dụ:

Với 4 phần tử Mai, Lan, Cúc, Trúc có thể xếp được bao nhiêu tổ hợp khác nhau, với mỗi tổ hợp gồm 2 phần tử ?

= COMBIN(4, 2) = 6

6 tổ hợp này là: Mai-Lan, Mai-Cúc, Mai-Trúc, Lan-Cúc, Lan-Trúc và Cúc-Trúc

1. Hàm EXP()

Tính lũy thừa của cơ số e (2.71828182845905...)

Cú pháp: = EXP(number)

number: số mũ của cơ số e

Lưu ý:

- Để tính lũy thừa của cơ số khác, bạn có thể dùng toán tử ^ (dấu mũ), hoặc dùng hàm POWER()

- Hàm EXP() là nghịch đảo của hàm LN(): tính logarit tự nhiên của một số

Ví dụ:

EXP(1) = 2.718282 (là chính cơ số e)
EXP(2) = 7.389056 (bình phương của e)